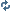|
|
|

Calgary25938 Posts
ㅡ_ㅡ;;
Edit: Please start the problem, or indicate the areas you are having trouble with. "SOLVE THIS OMG OLOLOL" is not an acceptable OP.
|
LAWL
EPIC SMILEY !
to topic: a agree with chill 
|
Strange to write the divergence as V•∇ - it's usually written with the gradient first, but dot product is commutative so it should be zero in any case. That makes the whole first term zero, so you essentially have to solve
∂V/∂t = v∇V - 1/ρ∇P + ƒ
The second term is independent of V (so it seems), so you just have to solve the basic form
∂V/∂t = v∇V - C
Which should be pretty straightforward.
|
FUck, i miss the days when i used to know stuff (and cared about capitalization on tl -.-)
|
On October 28 2008 22:25 jgad wrote:
Strange to write the divergence as V•∇ - it's usually written with the gradient first, but dot product is commutative so it should be zero in any case. That makes the whole first term zero, so you essentially have to solve
∂V/∂t = v∇V - 1/ρ∇P + ƒ
The second term is independent of V (so it seems), so you just have to solve the basic form
∂V/∂t = v∇V - C
Which should be pretty straightforward.
dot product is commutative for normal vectors, which contain (commutative) scalars and not derivatives, which are of course not commutative.
I wish I could help you Bluzman, but I did this stuff long time ago and I am not going to delve into it again for this one problem, it takes too much time.
Maybe you can simplify it by using the epsilon tensor (Levi-Civita symbol) and writing it out.
|
dot product is commutative for normal vectors, which contain (commutative) scalars and not derivatives, which are of course not commutative.
Yeah, I thought of this too, but it would seem that the first term would end up being
-(Vx∂/∂x + Vy∂/∂x + Vz∂/∂z)V
anyway, which would come out as :
-V(∇•V)
so I think -(V•∇)V = -V(∇•V) = 0 (given the second equation)
I could be wrong.
|
On October 28 2008 23:12 jgad wrote:Show nested quote +
dot product is commutative for normal vectors, which contain (commutative) scalars and not derivatives, which are of course not commutative.
Yeah, I thought of this too, but it would seem that the first term would end up being -(Vx∂/∂x + Vy∂/∂x + Vz∂/∂z)V anyway, which would come out as : -V(∇•V) so I think -(V•∇)V = -V(∇•V) = 0 (given the second equation) I could be wrong.
You are wrong, it is
-(Vx∂/∂x + Vy∂/∂x + Vz∂/∂z)Vx,
-(Vx∂/∂x + Vy∂/∂x + Vz∂/∂z)Vy,
-(Vx∂/∂x + Vy∂/∂x + Vz∂/∂z)Vz,
which is a vector in itself and that vector does not equal (0,0,0), atleast not because ∇•V=0 (scalar!)
|

Calgary25938 Posts
lol i got owned 
|
On October 28 2008 23:18 Maenander wrote:Show nested quote +On October 28 2008 23:12 jgad wrote:
dot product is commutative for normal vectors, which contain (commutative) scalars and not derivatives, which are of course not commutative.
Yeah, I thought of this too, but it would seem that the first term would end up being -(Vx∂/∂x + Vy∂/∂x + Vz∂/∂z)V anyway, which would come out as : -V(∇•V) so I think -(V•∇)V = -V(∇•V) = 0 (given the second equation) I could be wrong. You are wrong, it is -(Vx∂/∂x + Vy∂/∂x + Vz∂/∂z)Vx, -(Vx∂/∂x + Vy∂/∂x + Vz∂/∂z)Vy, -(Vx∂/∂x + Vy∂/∂x + Vz∂/∂z)Vz, which is a vector in itself and that vector does not equal (0,0,0), atleast not because ∇•V=0 (scalar!)
Yeah, you're right. So the first coordinate in the first term reduces to
-(Vx∂/∂x + Vy∂/∂y + Vz∂/∂z)Vx
= -Vx∂/∂x(Vx) - Vy∂/∂y(Vx) - Vz∂/∂z(Vx)
= -Vx(1) - Vy(0)- Vz(0)
= -Vx
and the same for the rest (y and z), so -(V•∇)V = -V, it would seem?
Anyway, I just noticed that the second term in the OP is ∆V and not ∇V - this seems confusing as it's either a typo or we need to know what ∆V is a delta of (V(t2) - V(t1)) or (V(x2) - V(x1)) - it could be anything.
|
∆ is the Laplace-Operator, I guess in the US you would write ∇ ^2.
And I don´t see why
-Vx∂/∂x(Vx) - Vy∂/∂y(Vx) - Vz∂/∂z(Vx) = -Vx(1) - Vy(0)- Vz(0)
should be correct.
edit: And I agree with chill here, Bluzman should show us his work, so we can point out errors. Again I am too rusty and too lazy to solve this (I should do other things anyway ^^).
|

United States24342 Posts
On October 28 2008 23:24 Chill wrote:lol i got owned 
I don't see you getting pwned. How did you get pwned?
|
Just interested in knowing what level physics this is?
|
looks like ~third year electrodynamics. Incompressible vector fields (∇•V=0) define the magnetic field or the electric field in regions of no space charge, for example.
|
On October 28 2008 23:50 Maenander wrote:
∆ is the Laplace-Operator, I guess in the US you would write ∇ ^2.
Weird, and yeah, I've only ever seen it as ∇^2.
Anyway, I agree that more information is needed about what these fields are supposed to be - if these are all general quantities which could be anything then I think the solution is going to be really messy.
And I don´t see why
-Vx∂/∂x(Vx) - Vy∂/∂y(Vx) - Vz∂/∂z(Vx) = -Vx(1) - Vy(0)- Vz(0)
should be correct.
Yeah, I'm trying to all of this too quickly. It occured to me just after I posted it, but yeah, there's no reason why V can't be Vx(x,y,z), Vy(x,y,z), Vz(x,y,z), in which case this all gets really horrible.
|
Russian Federation4235 Posts
Oh please help me, I'm so lost...
|
On October 29 2008 00:10 jgad wrote:
looks like ~third year electrodynamics. Incompressible vector fields (∇•V=0) define the magnetic field or the electric field in regions of no space charge, for example.
Fun, fun. 
|

United States3824 Posts
On October 28 2008 23:24 Chill wrote:lol i got owned 
I thought the smiley was quite nice actually. Aren't you only supposed to police the strat forums though?
|

United States3824 Posts
I've heard that in Russia you have to get the right answer to math problems. It must be nice eto have a mathematics conceptual system that isn't dumb as hell.
|
I know what this equation is - this is fluid mechanics, the Navier-Stokes equation! Good luck finding solutions - there's a million dollar prize if you do.
Got $1m?
|
|
|
|
|
|
![[image loading]](http://upload.wikimedia.org/math/e/9/1/e9155dcf8f9e3e3a58d34f757b121766.png)
![[image loading]](http://upload.wikimedia.org/math/2/3/3/23322e14d5f47462fd56523d8a5824b0.png)